Koordinationschemie II
Übung: IR-Spektrum und Struktur

Fe2(CO)9

IR-Spektrum

Das folgende IR-Spektrum wurde mit einer festen Probe, fein zerrieben in KBr, aufgenommen:

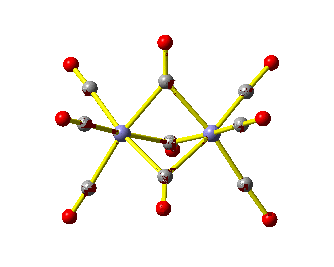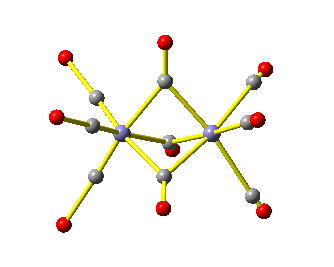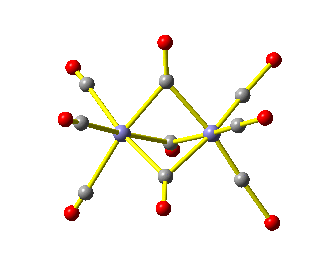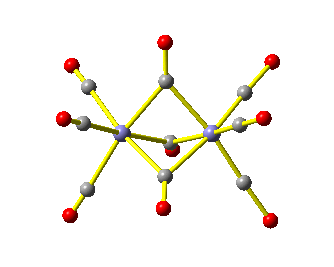
Die Intensitäten stimmen mit der Literatur überein, die Banden sind bis zu 20cm−1 verschoben. Im C-O-Valenzschwingungsbereich liegen zwei Banden vor, die terminalen CO-Gruppen zuzuordnen sind, und eine Bande im Bereich verbrückender Carbonylliganden. Ein vernünftiger Strukturvorschlag könnte so aussehen: [(CO)3Fe(μ-CO)3Fe(CO)3], die Molekülsymmetrie wäre dann D3h.

Charaktertafel von D3h

Um zu prüfen, ob das Auftreten von drei Valenz­schwingungs­banden mit der angenommenen Molekülsymmetrie verträglich ist, wird als Hilfsmittel die Charaktertafel von D3h benötigt. In der lehrbuchüblichen Fassung sind als Hilfe Funktionen enthalten, die wie die jeweiligen Rassen transformieren. IR-aktive Schwingungen, die eine Änderung des molekularen Dipolmoments erfordern, transformieren wie die Basisvektoren (x, y, z) – in D3h sind dies die Rassen E′ und A2′′.

D3h         E      2C3     3C2     σh     2S3     3σv      
A1′ 1 1 1 1 1 1     x2 + y2, z2
A2′ 1 1 −1 1 1 −1   Rz  
E′  2 −1 0 2 −1 0   (x, y) x2− y2, xy
A1′′ 1 1 1 −1 −1 −1      
A2′′ 1 1 −1 −1 −1 1   z  
E′′  2 −1 0 −2 1 0   (Rx, Ry) (xz, yz)

Valenzschwingungen

Da die Valenzschwingungen terminaler und verbrückender CO-Liganden deutlich getrennt voneinander vorliegen, wird die Symmetriebetrachtung für beide Ligandtypen getrennt ausgeführt (wenn dies nicht der Fall ist, betrachtet man alle Schwingungsvektoren zusammen). Zuerst die sechs terminalen Carbonylliganden, dann die verbrückenden. Es ergibt sich:

      E      2C3     3C2     σh     2S3     3σv
Γ6 6 0 0 0 0 2
Γ3 3 0 1 3 0 1

Verwendung der Reduktionsformel

Zur Reduktion von Γ6 verwenden wir am Besten die Reduktionsformel (hierzu gibt es auch eine detaillierte Übung am Beispiel des Ammoniakmoleküls). ni sind dabei die Faktoren vor den Symmetrieelemeten in der Titelzeile der Charaktertafel (1   2   3   1   2   3), χi ist 6   0   0   0   0   2. Der Beitrag jeder Rasse zur reduziblen Darstellung ergibt sich durch zeilenweises Summieren und Division durch Σni:

      E      2C3     3C2     σh     2S3     3σv   Summe   ×1/12
ni × χi × A1′ 6 0 0 0 0 6   12 1
ni × χi × A2′ 6 0 0 0 0 −6   0 0
ni × χi × E′  12 0 0 0 0 0   12 1
ni × χi × A1′′ 6 0 0 0 0 −6   0 0
ni × χi × A2′′ 6 0 0 0 0 6   12 1
ni × χi × E′′  12 0 0 0 0 0   12 1

Die gesuchten Rassen für die Valenzschwingungen der terminalen Carbonylliganden sind also A1′ + E′ + A2′′ + E′′. IR-aktive sind darunter E′ und A2′′, es werden also zwei Banden bei höherer Frequenz erwartet.

Für Γ3 ergibt sich mit den χi-Werten 3   0   1   3   0   1:

        E      2C3     3C2     σh     2S3     3σv   Summe   ×1/12
ni × χi × A1′ 3 0 3 3 0 3   12 1
ni × χi × A2′ 3 0 −3 3 0 −3   0 0
ni × χi × E′  6 0 0 6 0 0   12 1
ni × χi × A1′′ 3 0 3 −3 0 −3   0 0
ni × χi × A2′′ 3 0 −3 −3 0 3   0 0
ni × χi × E′′  6 0 0 −6 0 0   0 0

Das Ergebnis: A1′ + E′. Mit E′ als IR-aktiver Schwingung wird eine Bande bei niedrigerer Frequenz erwartet, in der Summe also drei Banden. Genau das wird beobachtet (in Klammern die Zuordnung der Publikation): 2064 (terminal A2′′), 2037 (terminal E′) und 1848 cm−1 (verbrückend E′).

Berechnung der Molekülschwingungen

Das Ergebnis lässt sich anschaulich darstellen, wenn die Schwingungen berechnet werden. Im Beispiel wird hierzu die Struktur des D3h-symmetrischen Moleküls auf B3LYP/tzvp-Niveau optimiert und anschließend eine Frequenzrechnung auf demselben theoretischen Niveau vorgenommen (wenn Sie nachrechnen möchten, können Sie die Gaussian-Eingabedatei fe2co9_vibr.gjf verwenden; für die Strukturoptimierung wird die Anweisung „opt“ anstelle von „freq“ verwendet; möchten Sie mit Orca rechnen, finden Sie hier die Eingabedatei; wenn Sie genau dasselbe wie mit Gaussian machen wollen, ändern Sie die erste Zeile zu: rks b3lyp rijcosx tzvp tzvp/j opt). Um das Gaussian-Ergebnis anzuschauen, können Sie die Ausgabedatei fe2co9_vibr.out mit GaussView ansehen. Trotz des „billigen“ Basissatzes ist das Ergebnis hinsichtlich der Frequenzen verwertbar, man beachte aber die grobe Abweichung bei den Intensitäten:

    exp./cm−1   DFT   ×0.965   Intensität(DFT)/%
A2′′ 2064 2133 2058 100
E′ 2027 2114 2040 68
E′ 1848 1921 1854 42

Bei der Visualisierung sieht dann zum Beispiel die A2′′-Schwingung so aus: