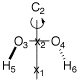
This point group contains only two symmetry operations:

E    the identity operation
C₂   a twofold symmetry axis

A simple example for a C₂ symmetric molecule is hydrogen peroxide (H₂O₂), here in its HF/6-31G(d) optimized structure:

#P HF/6-31G(d) opt=(Z-Matrix,tight) test1 HF/6-31G(d) opt H2O2 0 1 x1 x2 1 1.0 O3 2 r3 1 90.0 O4 2 r3 1 90.0 3 180.0 H5 3 r5 2 a5 1 d5 H6 4 r5 2 a5 1 d5 r3=0.69822676 r5=0.94920388 a5=102.078438 d5=58.0069855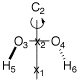

The symmetry of the system is reflected in the Z-Matrix containing two dummy atoms x1 and x2 located on the principal symmetry axis. Use of the symmetry properties speeds up energy calculations, reduces the number of independent structural variables from 6 (for an asymmetric, non-linear molecule containing four centers) to 4 and thus accelerates geometry optimizations.

Molecular orbitals as well as harmonic vibrations (if calculated) are labeled according to their symmetry properties as belonging to one of the two irreducible representations (A and B) of the C₂ point group. Those properties belonging to irreducible representation A are symmetric to both the identity operation E as well as the 180 degree rotation around the C₂ axis. Those properties belonging to irreducible representation B are symmetric with respect to the identity operation E, but antisymmetric with respect to rotation around the C₂ axis.

last changes: 24.04.2009, HZ
questions & comments to: zipse@cup.uni-muenchen.de